Gaussian vs. Neural Net

Felix Bogdanski, since 11.1.2016

In Artificial Neural Networks we studied the core concepts of these powerful, universal approximators. In this article, we research how a neural net can be used instead of a gaussian for basic predictive analysis. You can check the code and data on GitHub.

This data set from the University of California aggregates US census income data from 1994. The data set counts 32461 rows, which is roughly 4MB. Being a multivariate data set, we could pick arbitrary combinations of features for our model. To keep things simple, we work with only age and a boolean, indicating if a person makes more than 50K a year. In the end, we want a probability of earning more than 50K a year with respect to age. 

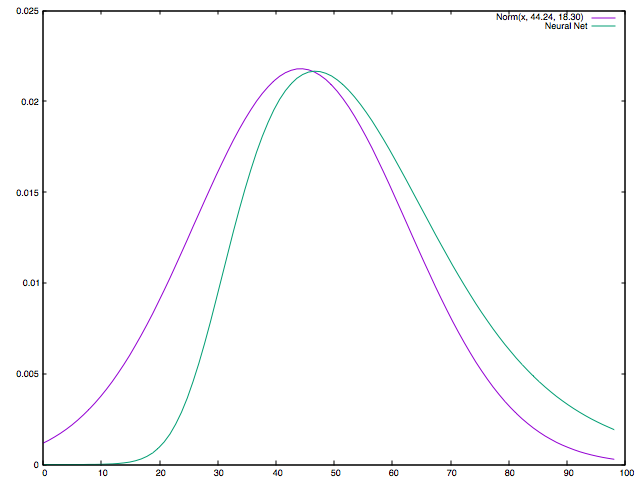
  26, Private, 94936, Assoc-acdm, 12, Never-married, Sales, Not-in-family, White, Male, 0, 0, 40, United-States, <=50K
  38, Private, 296478, Assoc-voc, 11, Married-civ-spouse, Craft-repair, Husband, White, Male, 7298, 0, 40, United-States, >50K
  36, State-gov, 119272, HS-grad, 9, Married-civ-spouse, Protective-serv, Husband, White, Male, 7298, 0, 40, United-States, >50K
  33, Private, 85043, HS-grad, 9, Never-married, Farming-fishing, Not-in-family, White, Male, 0, 0, 20, United-States, <=50K
  22, State-gov, 293364, Some-college, 10, Never-married, Protective-serv, Own-child, Black, Female, 0, 0, 40, United-States, <=50K
  43, Self-emp-not-inc, 241895, Bachelors, 13, Never-married, Sales, Not-in-family, White, Male, 0, 0, 42, United-States, <=50K
  ...
Since census data means people and the law of large numbers, things often turn out to be under a normal distribution. Let's for now forget about the neural net and build a predictive model with the good, old gaussian:

While being a clever way of drawing a bell curve, the gaussian is inherently unimodal and, because of the square within the functional dependency, symmetric. Indeed, a very perfect function — but maybe too perfect for nature?

The plot has mean , it is the average age of people earning more than 50k. Chances are higher for this person to be 44 than 18 years. Sounds pretty reasonable. But my gut tells me there is something wrong about the symmetry. Is it true, that 18 and 70 agers earn the same? Intuitively, I would say no, if a person is 70 years old, he or she earns more money than the average kid of 18 years. Think of pension income, interest income, or even a regular job. Maybe, the gaussian is just too perfect to explain nature.

Let's build a more natural model using our beloved neural nets. We choose layout , so 1 neuron for the input age, 20 neurons for the dense layer and one neuron for the output boolean encoded as : 

  val src = scala.io.Source.fromFile(getResourceFile("file/income.txt")).getLines.map(_.split(",")).flatMap { k =>
    (if (k.length > 14) Some(k(14)) else None).map { over50k => (k(0).toDouble, if (over50k.equals(" >50K")) 1.0 else 0.0) }
  }.toArray

  val f = Sigmoid

  val network = Network(Vector(1) :: Dense(20, f) :: Dense(1, f) :: SquaredMeanError())

  val maxAge = train.map(_._1).sorted.reverse.head

  val xs = train.map(a => Seq(a._1 / maxAge))
  val ys = train.map(a => Seq(a._2)) // Boolean > 50k

  network.train(xs, ys)
Furthermore, we need to map the age to domain , because this is where the sigmoid operates on. So, we divide by maximum age and start training. After a couple of seconds, and a cup of sencha, training with 2000 samples succeeds, so we can normalize and plot both models:

Comparing the gaussian with the net, we notice a slight difference between them. While the gaussian is not able to capture the asymmetry, our net can capture this shape in a natural way. The gaussian works with mean and variance to fit a training set. However, the gaussian shape will always dominate, because of its functional form. A neural net, on the other hand, learns the underlying data. If, for instance, our data set was multimodal, i. e. with two peaks, the gaussian would give poor results, whereas the neural net would be able to capture it. Thanks for reading.